Multiplication and Division -
Introduction to Division

Multiplication and Division
Introduction to Division


/en/multiplicationdivision/video-multiplication/content/
Division is splitting something equally. For instance, let's say you have 10 raffle tickets, and you'd like to share them with 5 friends.
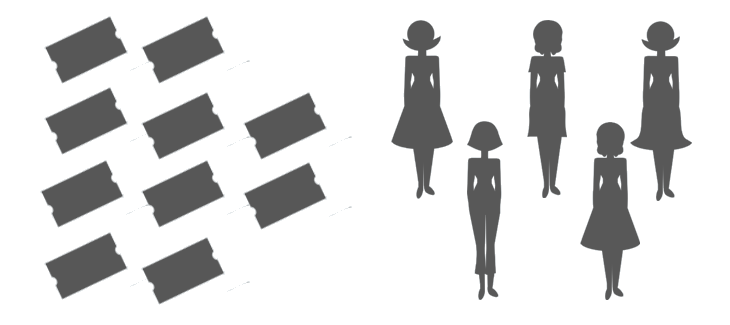
You divide the tickets among your friends. Each friend gets an equal number of tickets.

See how they each have 2 tickets? When you divide 10 tickets among your five friends, you create 5 equal groups of 2 tickets.
Division happens a lot in real life. For instance, consider the situation below.
In the slideshow, you saw that we divided six cupcakes into two equal groups. To figure out the number of cupcakes that are in each group, you could write a division expression like this:
6 / 2
You could also write the expression like this:
6 ÷ 2
You can read either expression as six divided by two. The division sign (/ or ÷) means something is being divided. This is why we always put it after the first number — there were 6 cupcakes, and we divided them into 2 groups.
Many real-life situations can be expressed with division. For example, imagine you're placing 15 cans on 3 shelves. You can divide to make sure you put the same number of cans on each shelf. In other words, 15 cans divided by three shelves, or 15 / 3.

Try setting up these situations as division expressions. Don't try to solve them yet.
A teacher has 16 pencils that she distributes evenly between 4 students.
A florist has 18 roses and divides them equally between 3 vases.
You have 6 treats to share equally with your 3 dogs.
You can use counting to solve simple division problems. For instance, let's say we have 12 seedlings. We decide to plant them in two even rows. How many plants go in each row? We could write that question like this:
12 / 2
Remember, that expression means 12 divided by two, or 12 seedlings divided into 2 rows. It's a simple problem. To solve it, you can put the seedlings into two groups and then count how many plants are in each group. The answer is 6. We know that 12 / 2 = 6.

While counting works for problems that begin with small numbers, a problem that begins with a large number can take a long time to solve with counting. For this reason, most people memorize common division problems so that they can solve them quickly. If this sounds hard, don't worry. With some practice, you'll be able to quickly remember the answers.
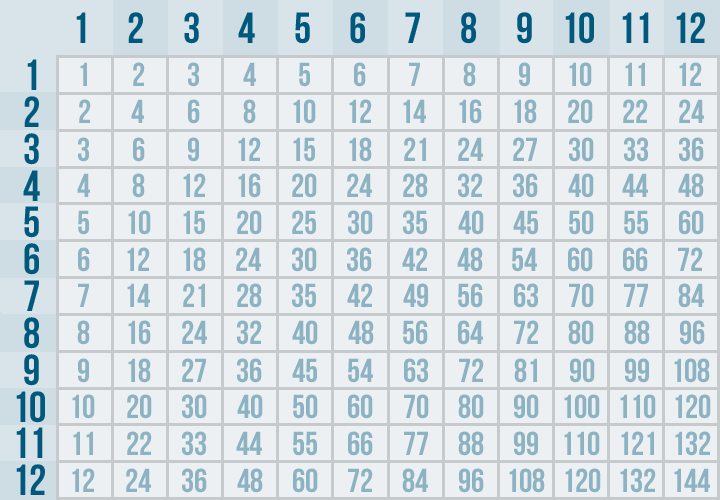
In Introduction to Multiplication, you were introduced to the times table. In that lesson, you used it to solve multiplication problems. You can also use the times table to solve division problems.
Let's start with a problem we're already familiar with. How would we have solved the seedling problem with the times table?
Click through the slideshow below to learn how.
Solve these division problems. If you need some help, you can use the times table.
In the previous pages, we divided numbers equally. For instance, at the beginning of the lesson, we divided 10 tickets equally between 5 people. Each person received 2 tickets. What happens when a number can't be equally divided?
For example, consider the situation below.
You can see from the slideshow that the remainder (1) is smaller than the number we divided by (3). That will always be the case when the problem has a remainder. For example, look at each of these problems below:
21 / 5 = 4 r1
The remainder of 1 is smaller than 5.
76 / 6 = 12 r4
The remainder of 4 is smaller than 6.
If the remainder is larger, that means the amount left over is too large. You'll need to try dividing again. For example, if you have 4 friends and 7 tickets left over, you know that each friend can get at least one more ticket.
Practice division with these problems. If you'd like, you can use the times table for help. There are 3 sets of problems with 5 problems each.



/en/multiplicationdivision/long-division/content/