Decimals -
Introduction to Decimals
Decimals
Introduction to Decimals
search
menu
A decimal is another way to write a fraction. You can think of a decimal as a part of a whole number. It is less than 1 whole thing, but more than 0.
You may not realize it, but you see decimals a lot in real life. One of the most common examples is money.
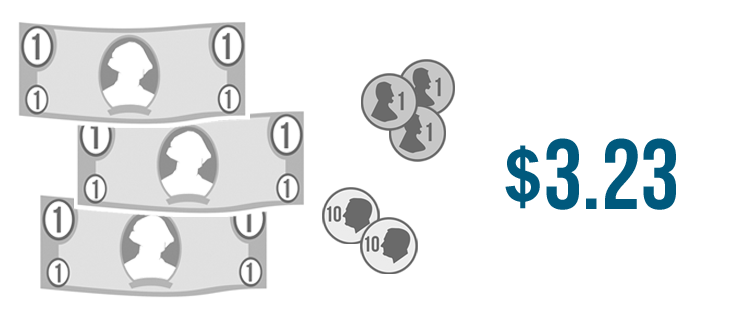
Do you recognize these coins? We have a quarter, a dime, and two pennies. You could write each of these as a decimal. That's because each coin is worth less than a whole dollar.
Click through the slideshow to learn how decimals work.
This is a dollar. A dollar represents a whole number. It is equal to 1.
We could also write that as 1.00. In other words, 1 = 1.00.
1.00 is a decimal. Here, it means we have 1 dollar and 0 cents.
As you may already know, there are 100 pennies in a dollar. This means 100 pennies equals 1.00.
One penny is part of a dollar. More specifically, it's 1 cent. We could also write that as a decimal: 0.01.
Let's look at a few more decimals. 9 cents is 0.09 of a dollar.
A quarter, or 25 cents, is 0.25 of a dollar. Any time you have part of a whole, you can write it as a decimal.
Let's look at another example. This pitcher holds 1 liter of water. Right now it's full.
We could write this as a decimal: 1.00 liters.
The pitcher is split into 10 parts. This means each part is equal to 0.10 liters.
As the day goes on, the pitcher gets emptier. Now it has 0.70 liters. That's because we used up 0.30 liters.
Now it has 0.50 liters, or half a liter.
Now it has 0.20 liters. Even though we have less than one liter, we have more than zero liters, so we can write it as a decimal.
As you saw on the last page, decimals look a lot like a regular numbers, with a few important differences. First, all decimals have a decimal point (.). The decimal point looks like a period. Any number to the left of the decimal point is a whole number. The numbers to the right are like a fraction—they're less than 1 whole but more than 0.
For example, let's take a look at this decimal.
9.6
9 is on the left of the decimal point, so we have 9 whole things. 6 is on the right, so we also have 6 parts of a whole.
We see written decimals all the time in real life. For example, you might know that the average body temperature is 98.6 degrees. Or you might tune in to a radio station like 97.5. But do you know how to read these decimals out loud?
Click through the slideshow to learn how to read decimals.
Let's try reading this decimal: 9.6.
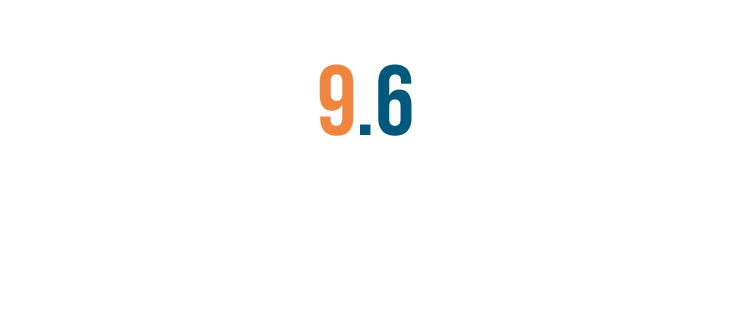
First, we'll read the number to the left of the decimal point. That's nine.
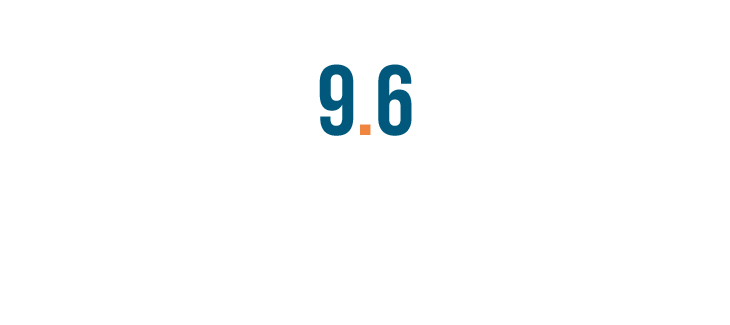
Next, we'll read the decimal point. Usually, you'll just say "point".
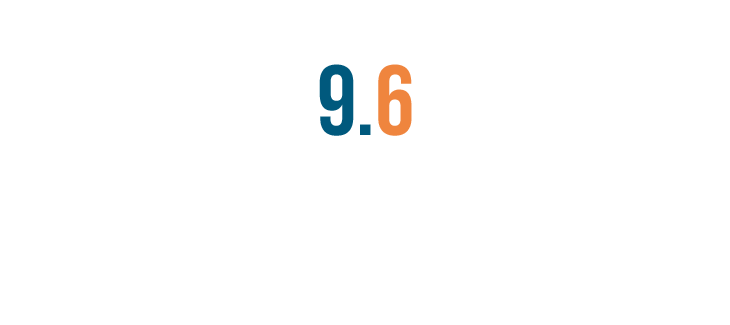
Finally, we'll read any number to the right of the decimal point. That's six.
So, we'd read 9.6 like this: nine point six.
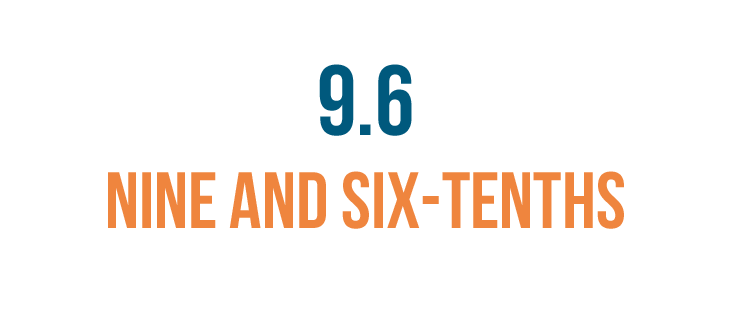
But you could also read it like this: nine and six-tenths.
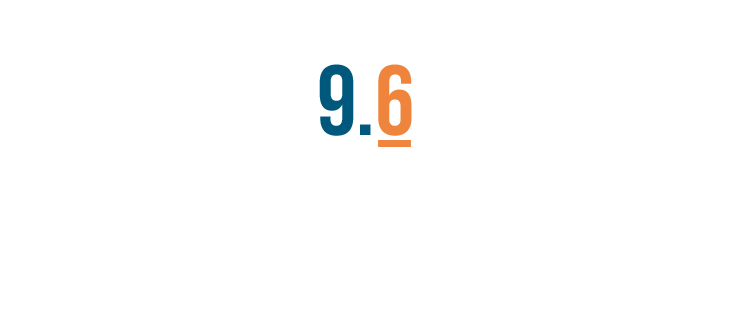
When you read decimal numbers, each place to the right of the decimal point has a special name.
The place immediately to the right of the decimal point is the tenths place.
Here, the decimal means we have .6, or six-tenths, of a whole.
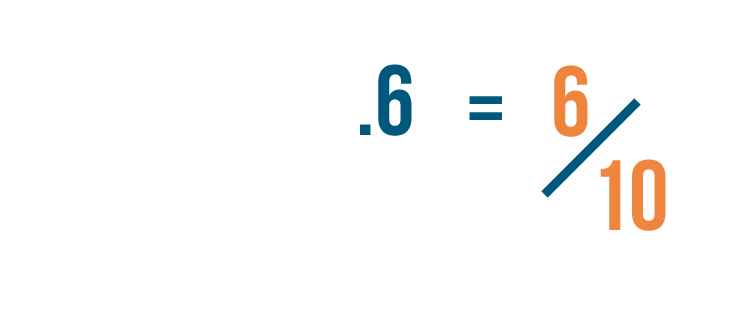
You might remember from Introduction to Fractions that six-tenths is just another way of saying 6/10.
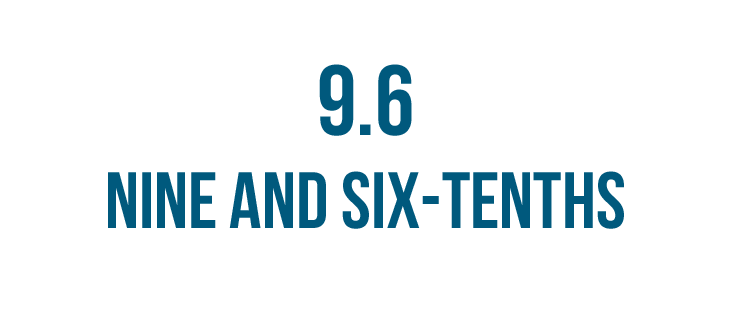
So 9.6 means we have 9 whole things and 6/10, or six-tenths, of another thing.
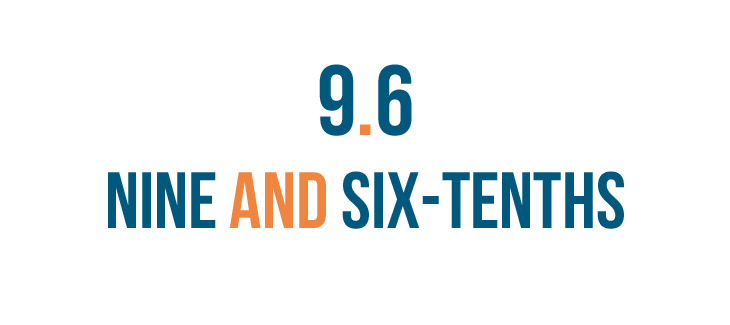
Since we have nine and six-tenths, the word "and" replaces the decimal point.
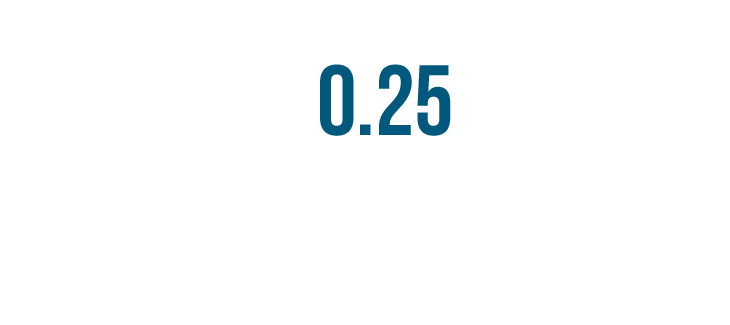
Let's try another example. How would you read this decimal? 0.25.
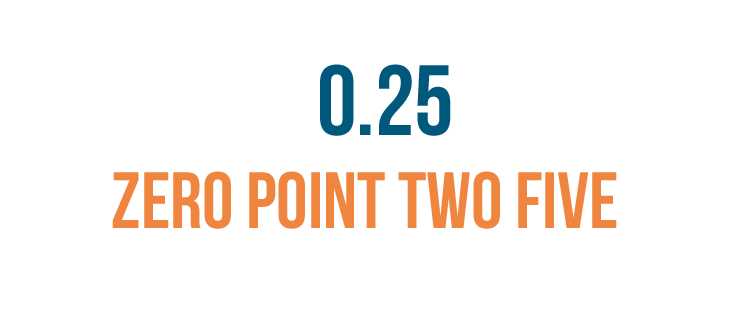
We can read 0.25 as zero point two five...
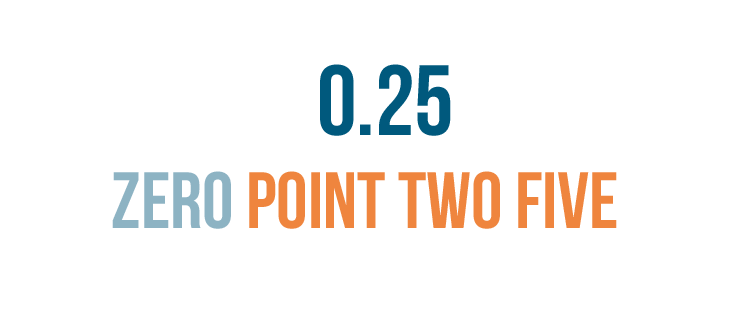
We can read 0.25 as zero point two five...or leave out the zero and just say point two five.
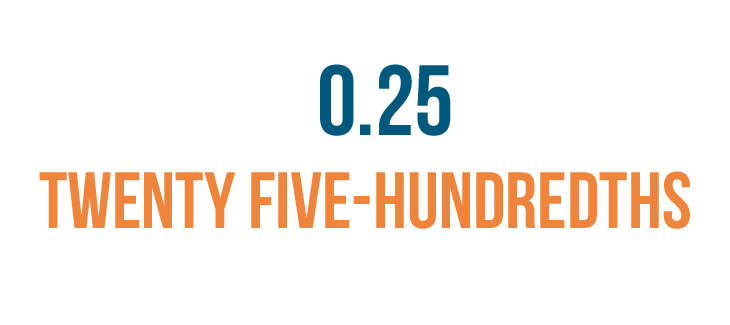
But we could also read it like this: twenty five-hundredths.
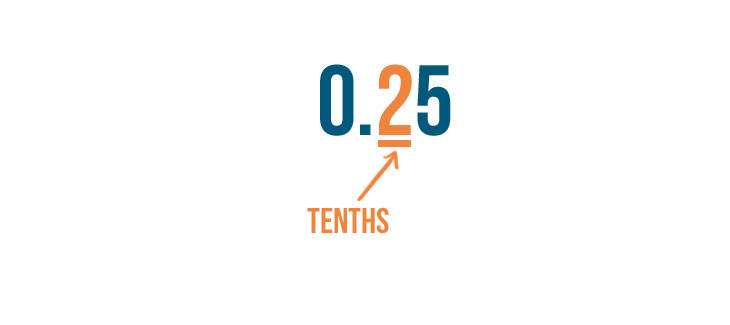
Let's look at our decimal places again. 2 is in the tenths place, so we have two-tenths.
Next is the hundredths place. In this example, 5 is in the hundredths place, so we have five-hundredths.
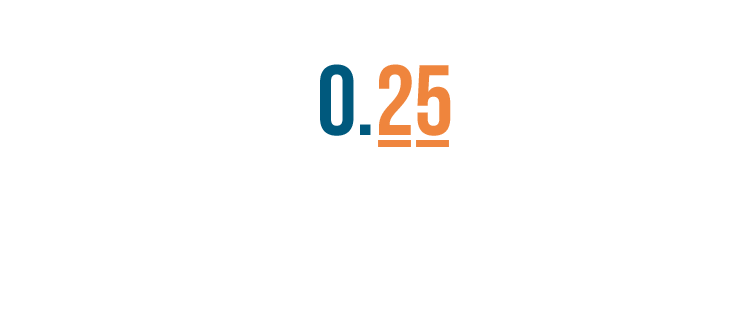
When we read this number aloud, we'll say the 2 and 5 together as "twenty-five".
We'll also say the decimal place that is farthest to the right. In our example, that's the hundredths place.
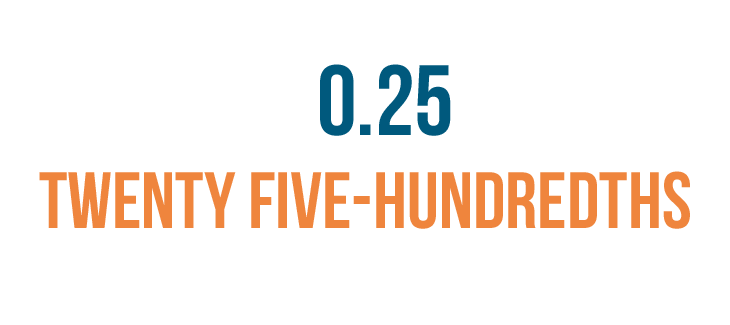
So we'll read 0.25 as twenty five-hundredths.
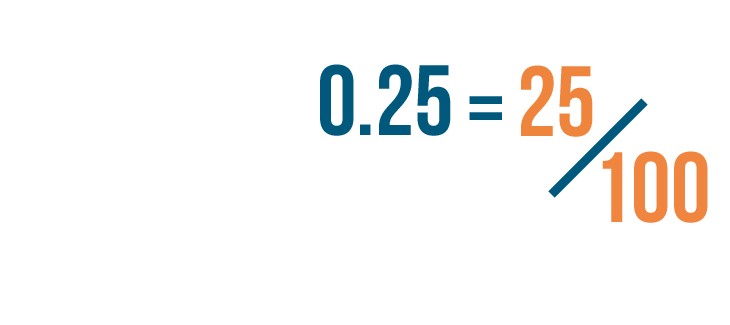
This is just another way of writing 25/100.
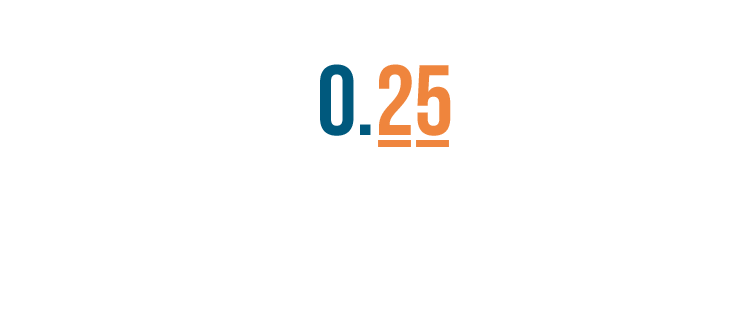
To figure out how many hundredths we had total, we could have added these numbers: two-tenths and five-hundredths.
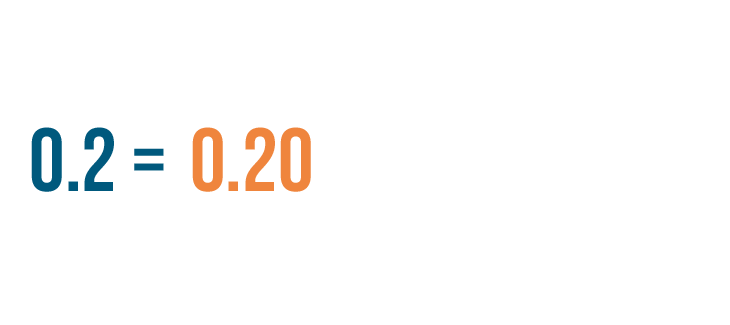
2 tenths is the same as 0.20, or twenty-hundredths.
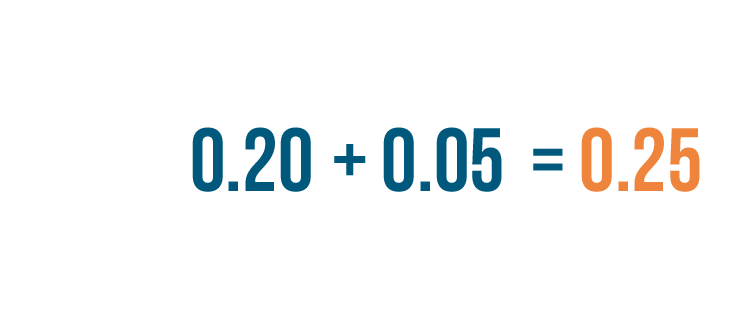
0.20 plus 0.05 equals 0.25, or twenty five-hundredths.
Try reading the decimals below aloud.
What if you had to read this decimal out loud?
Even though we use decimals when we use money, we read them slightly differently. Instead of three point two three, or three and twenty three-hundredths, we'll say three dollars and twenty-three cents.
You could also read it like this: "three twenty three". To save time, most people leave out the decimal point when talking about money. How about $5.99? That would be five dollars and ninety-nine cents, or five ninety-nine.
Remember, these rules only work with money. They can't be used to read other decimals.
Try reading these dollar amounts.
Let's imagine you're shopping for a new water pitcher. You find two you like—one holds 0.7 gallons, while the other holds 0.5 gallons. Do you know which pitcher is larger? Click the arrows to find out.
To find out which pitcher holds more, you could simply compare the decimals to see which is larger.
7 is larger than 5, so 0.7 is larger than 0.5. The larger the number to the right of the decimal point, the larger the decimal.
Again, you'll simply compare the numbers to the right of the decimal point.
74 is larger than 72, so 0.74 is larger than 0.72.
Since the whole number, 1, is the same for both decimals, we'll compare the numbers to the right of the decimal point.
If you thought .2 was larger than than .19, you were right!
Remember, 1.2 could also be written as 1.20.
20 is larger than 19, so 1.20 is larger than 1.19.
/en/decimals/adding-and-subtracting-decimals/content/
